Kinematics Optimization for Redundant Manipulators

Introduction

Motivation

The 7DoF(seven-degree-of-freedom) robotic arm not only possesses the excellent characteristics of redundant DoF but also maintains the high rigidity. Due to the extra DoF, the 7DoF redundant robotic arm has good fault tolerance, singularity position avoidance, and torque optimization. By constructing an optimization model, achieving good dynamic performance of the robotic arm, it can ensure smooth joint movement while completing specific tasks under physical, hardware, and control constraints.

Quadratic Programming (QP) can be widely used in industrial applications. Many practical engineering problems can be converted into QP problems for solution. Therefore, QP problems and their solutions are widely and deeply researched by researchers and engineering application personnel.

In previous research, generally only situations subject to one or two typical constraints (such as linear equations and inequality constraints) are discussed. However, the quadratic programming problems in actual engineering applications are often subject to multiple constraints at the same time: equation constraints, inequality constraints, and double-ended constraints. This project is to convert the specific tasks of the redundant robotic arm into quadratic programming problems and achieve optimization under various constraints.

Related Work

Redundant DoF robots, while ensuring the end-effector motion law, use self-motion in the null space to generate different configurations, thus enabling the robot to use the redundant degrees of freedom to avoid obstacles, overcome singularity, improve flexibility, and achieve better dynamic performance. Because of their inherent advantages, many scholars have conducted extensive research on this topic, achieving impressive results.

The main content of the research includes: how to use the extra degrees of freedom of redundant robots to improve the robot’s kinematic and dynamic characteristics, such as increasing flexibility, avoiding obstacles, overcoming singularity, optimizing auxiliary operation indicators under the main motion task, and optimizing joint speed, acceleration, torque, energy, etc.

My Contribution

For a specific task where the object moving along the specified planned trajectory, the camera located at the end of 7DoF redundant robotic arm needs to track it in real time, under the physical constraints of joint angles, angular velocity, etc., while ensuring that the camera moves at the minimum speed in Cartesian space.

My task is setting up an object trajectory planning framework, writing 7DoF kinematics code and implementing the inverse kinematics framework, and converting this specific task into a quadratic problem and implementing the code and successful simulation in the simulation environment. At the same time, in some unsolvable situations during the camera view tracking process, I introduce slack variables and define task priorities (high priority is camera view tracking objects, low priority task is to optimize end speed), and finally successfully implement the optimization of the QP in the specific task of the redundant robotic arm.

The target function defined is the speed of the end camera, and the control quantity is the joint angular velocity. After quadratic programming, the optimized target function is shown in Figure b, and the first two seconds of Figure b correspond to the situation where QP has no solution under constraints, that is, the slack variable in the first two seconds of Figure a is not zero. The figure shows the change of two values in the simulation results after QP solving under the conditions of high priority for the camera view tracking objects, low priority for optimizing the end speed, and the tracking object has a definite motion plan.

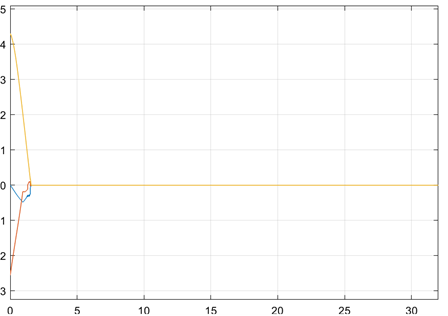
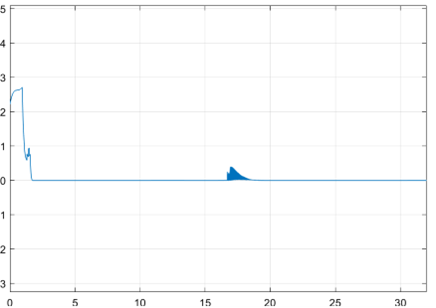
The following video shows the simulation of task in MATLAB Simscape under QP.